近日,中国科学院西安光学精密机械研究所副研究员曾健华团队等在分数衍射系统中的非线性波局域理论研究方面取得进展,研究成果以Localized modes in nonlinear fractional systems with deep lattices为题,在线发表于Advanced Theory and Simulations。
从高等数学中可知,积分学(也叫整数积分)是一种关于整数阶积分和导数的普遍形式理论。而于半个世纪前在数学中首先提出的“分数积分”,顾名思义,就是关于分数阶积分和导数的理论。近年来,随着物理学前沿研究的深入和发展,分数积分不再是“束之高阁”的数学理论,而可以用来描述实际的物理情景,比如在量子力学、光学、量子物理(含超冷原子)和凝聚态物理中的一些动力学特性都可以用具有分数衍射项的理论模型描述。在经典的量子力学中,描述粒子扩散的基本方程由基于布朗运动的费曼路径积分理论描述(整数阶积分);然而,对于非布朗运动路径,相应的本征方程变成分数阶积分的扩散方程。值得一提的是,加拿大科学家Nick Laskin在本世纪初研究发现,当费曼路径积分中的布朗运动轨迹由“随机行走”轨迹代替时,粒子的运动完全由空间分数衍射薛定谔方程描述。基于此发现,Nick Laskin发展了“分数量子力学”理论,并于2018年发表了著作Fractional quantum mechanics。
曾健华团队近年来在在分数衍射介质中激光和物质波的非线性局域理论方面取得了系列研究进展【Opt. Lett. 44, 2661 (2019); Non. Dynamics 98, 985(2019);Ann. Phys.(Berlin) 532, 1900385 (2020) ; Chaos 30, 063131(2020); Commu. Phys. 3,26(2020); Chaos, Solitons & Fractals 140, 110271(2020)】,揭示了丰富的局域模结构和非线性物理。然而,目前所有关于含周期势的分数衍射系统中的非线性理论都是局限于浅晶格或中度调制晶格,而关于深晶格情况下的非线性波局域理论尚未见报道。
周期结构中的非线性波动力学方程通常由两种方法描述:耦合模方程组和离散形式的非线性薛定谔方程。然而这两种方法都存在局限性,前者只能描述浅晶格,后者只能描述深晶格且仅适用于位于第一带隙的非线性波局域情形。本质上,紧束缚近似下的离散形式只能采用二次量子化下的瓦尼尔态函数描述最近邻势阱中的粒子耦合,而从第一性原理出发的连续性非线性薛定谔方程可以描述所有情形(非局域空间衍射项、多个势阱间的量子隧穿、高阶带隙等)。
研究团队从平均场近似下的连续性方程出发,系统性研究了囚禁于深晶格中的超冷原子非线性局域模的产生、特点和稳定性情况,重点探讨了在自散焦三阶非线性(对应于光学中的克尔效应)作用下位于第一带隙和第二带隙的带隙孤子和带隙涡旋的物理特性。理论上推导了归一化的动力学方程,借助托马斯-费米近似方法得出了物质波局域模的近似解析解,获得了(形成带隙孤子的)冷原子个数与化学势、衍射系数之间的依赖关系;计算结果表明,这些理论与数值结果能较好地吻合,揭示了深晶格具有强局域特性的物理机制(图1),线性衍射关系图显示其线性布洛赫能带是极平带,此时物质波群速度接近为0,因此绝大部分原子就被局域在最小晶格周期内。进一步研究发现,由于这一强局域特性,囚禁于深晶格的带隙孤子紧紧束缚在单晶格周期内(图2),这与自聚焦离散模型中分布于数个晶格周期内的离散孤子结果完全不同。通过线性稳定性分析和含微扰的直接数值模拟方法,研究发现带隙孤子和带隙涡旋都具有极好的“鲁棒性”。既往文献报道认为囚禁于浅晶格的不稳定局域模会快速坍塌,该团队研究发现在深晶格背景下,不稳定的局域模在演化过程中不会发生坍塌现象,只是在近邻晶胞产生旁瓣,因为此时相邻晶格周期内只存在较弱的量子隧穿效应(图3)。相关研究工作得到国家自然科学基金的支持。

图1 (a)二维实空间中深晶格局域超冷原子示意图;(b)随衍射系数变化的线性能带结构变化图;(c)对应二维动量空间中的简约布里渊区和高对称点;(d)浅晶格(蓝色虚线)和深晶格(黑色实线)情况下的线性衍射关系
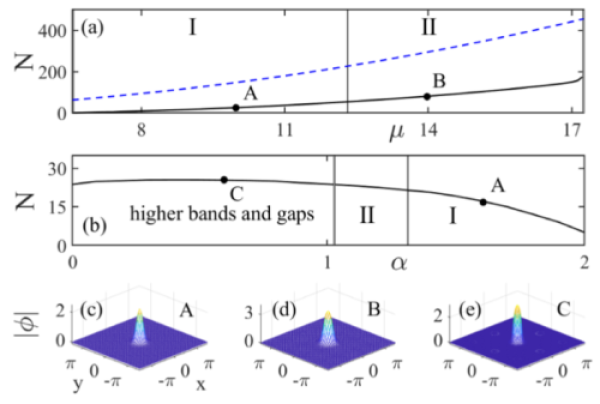
图2 (a)囚禁于深晶格中的物质波带隙孤子的原子数与化学势的关系图(蓝色虚线为托马斯-费米近似解析结果);(b)原子数与衍射系数的关系图;(c, d, e)仅局限于单晶格周期内的带隙孤子
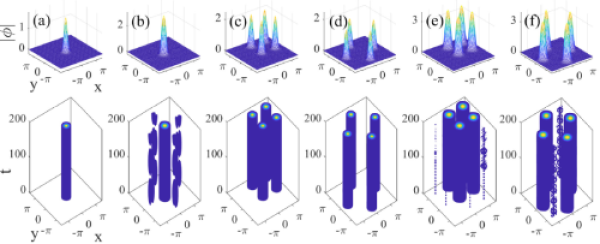
图3 上图:稳定(a)和不稳定(b)的物质波带隙孤子、稳定(c, d)和不稳定(e, f)的带隙涡旋;下图:微扰动力学演化图




